อสมการวิชาที่ว่าด้วยเรื่องความไม่เท่าเทียม พอได้เริ่มศึกษาไปลึกๆ ก็จะพบว่ามันมีทฤษฏีอะไรให้ได้รู้ได้เรียนกันมาก ไม่ได้มีแค่อสมการพื้นฐาน แบบ ตาม ม.3 ม.4 ทั่วไป ยิ่งเรารู้มากเราก็ยิ่งทำโจทย์ปัญหาได้หลากหลายมากขึ้น วันนี้เราจึงพยายามสรุปรวมทฤษฏีที่เราเคยได้ศึกษามาเอาไว้ให้ดูกันทีเดียว เอาแค่ที่นึกออกตอนนี้ (เพราะเจอมาเยอะ แต่จำไม่ค่อยได้) เดี๋ยวถ้านึกออกเพิ่มก็จะมาอัพเพิ่มเติมให้นะครับ หรือใครคิดว่า มีทฤษฏีอะไรอีกก็ลองบอกกันมาได้
อย่างไงก็ตามเราก็ยังเชื่อในการทำแบบฝึกหัดมากๆ มันจะช่วยให้เราได้ประสบการณ์ เพิ่มความสามารถเราได้อย่างเห็นผลชัดที่สุดแน่ๆ ครับ
อสมการนี้ เรื่องก็กล่าวถึงค่าเฉลี่ยสามตัวนั้นก็คือ ค่าเฉลี่ยเลขคณิต(Arithmetic Mean) ค่าเฉลี่ยเรขาคณิต(Geometric Mean) และค่าเฉลี่ยฮาร์มอนิก(Harmonic Mean) เป็นอสมการที่ใช้ง่ายหลากหลาย เราสามารถเลือกอะไรก็ได้มาแทนก็ได้ ควรจะรู้ไว้เป็นอันดับแรกๆ เรื่องก็มีอยู่ง่ายๆว่า
Arithmetic Mean(A.M.) จะมากกว่าหรือเท่ากับ
Geometric Mean(G.M.) จะรองลงมา มากกว่าหรือเท่ากับ
Harmonic Mean(H.M.) จะน้อยสุด
อสมการ โคชี่-ชวาร์ซ (Cauchy-Schwarz inequality)
บางคนเรียกแค่ "อสมการโคชี่" ก็ให้เข้าใจว่าหมายถึงตัวนี้ เป็นอสมการที่ใช้การอสมการที่ส่วนใหญ่มีเลขกำลังสองอยู่
อสมการนี้เป็นอีกตัวที่ ตัวที่ค่อนข้างพื้นฐาน ควรรู้ไว้ ใช้ได้หลากหลาย
อสมการค่าเฉลี่ยเลขคณิต เรขาคณิต แบบถ่วงน้ำหนัก (Weighted A.M.-G.M.)
อสมการที่สำคัญอีกตัว พัฒนามาจาก A.M.-G.M. ธรรมดา
แต่ขยาย ให้ใช้กันนอกเหนือจากจำนวนเต็มเป็นจำนวนจริงบวก
อสมการเจนเซน (Jensen inequality)
เป็นอสมการว่าด้วยเรื่องของฟังก์ชั่นนูน ฟังก์ชั่นเว้าหรือ Convex Concave function
ใช้แก้ปัญหาอสมการ ประเภทที่มีลักษณะเป็น Pattern วนๆ แล้วก็ลงสมมุติฟังก์ชั่น ให้มีลักษณะเป็นแบบ Pattern นั้น
ถ้าฟังก์ชั่นเป็น Convex ก็จะเป็นแบบข้างต้น แต่ถ้าฟังก์ชั่นเป็น Concave ผลที่ได้ก็จะตรงข้ามกันนั้นคือ เปลี่ยนเป็นเครื่องหมายน้อยกว่าเท่ากับ
แล้วเราจะรู้ได้ไงว่าอะไรเป็น Convex Concave
เอาเป็นง่ายๆ ละกันครับการที่ฟังก์ชั่นที่จะเป็น ฟังก์ชั่น Convex บนช่วงปิด [a,b] ได้นั้นคือการที่
ถ้าเราลากเส้นจาก จุด f(a) ไปยัง f(b) บนเส้นกราฟ จะสังเกตเห็นว่า เส้นที่ลากนั้นอยู่สูงกว่าเส้นกราฟตลอด
และถ้าเป็น Concave ก็เส้นจะอยู่ใต้กราฟตลอด
แต่การดูอย่างงี้เราก็ต้องไปวาดกราฟซึ่งอาจจะยุ่งยาก
เราจึงมีการตรวจสอบด้วยการ ดิฟสองครั้ง แล้วเอาค่า ใน [a,b] ไปแทน ถ้ามีค่ามากกว่า 0 ตลอดก็จะเป็น Convex บน [a,b]
อสมการของเชิร(Schur inequality)
บางคนอาจจะสงสังว่า cyc คืออะไร จริงแล้วมันก็คือผลบวก ของแต่ละพจน์ ที่เป็นการสลับตัวแปรกันของอีกพจน์ แค่นั้นเอง
อสมการของแบนูลี(Bernoulli inequality)
อสมการต่อไปเราต้องมาทำความเข้าใจกับนิยามอะไรกันนิดหน่อยก่อน เพื่อความสะดวก และความเข้าใจที่ตรงกัน
อสมการมูรเฮด (Muirhead inequality)
อสมการนี้เหมือนเป็นอะไรที่ใช้เพิ่มความสะดวก เห็นตัวนี้แล้วรู้สึกตัวว่าเรามั่วใช้ Am.Gm.Hm.อยู่ได้ ลำบากก็ลำบาก ส่วนมากมักจะใช้แบบโจทย์ที่มีการวนกันจนครบทุกตัวแปร
อสมการคารามาตา(Karamata inequality)
อสมการผสมกันระหว่าง Majorizartion และสมบัติความเป็น Convex Concave function เรียกได้ว่าไม่งงเราไม่ทำ
อสมการการจัดเรียง(Rearragement inequality)
เรื่องง่ายๆ ก็เอามาแก้ปัญหาอสมการได้หลายต่อหลายข้อด้วยกัน การจะแก้ปัญหาด้วยทฤษฏีนี้ส่วนมากเราต้องสมมุติให้อะไรมากกว่าหรือน้อยกว่าอะไร แต่มันก็มีข้อแม้ว่าการสับเปลี่ยนตัวแปรไปเราจะได้อสมการเดิม
อสมการเชบีเชฟ(Chebyshev inequality)
อีกอสมการที่มีลักษณะคล้ายกับสมการการจัดเรียง เนื่องมาจากเคยพูดถึงความยิ่งใหญ่ของผู้คิดค้นไปแล้วจึงไม่ขอกล่าวอะไรมากไปตามดูเอาเองละกัน Chebyshev
อสมการโฮเดอร์ (Holder inequality)
อสมการคล้ายกับอสมการโคชีข ชวาร์ซ แต่มีลักษณะเป็นกรณีที่ทั่วไปกว่าคือไม่จำเป็นต้องยกกำลังสองอย่างเดียวและสามารถยกกำลังเลขใดๆก็ได้
อสมการมินคอฟสกี (Minkowski inequality)
อสมการที่มีลักษณะคล้าย อสมการสามเหลี่ยม(Triangle inequlity) เพียงแต่ถ้าเป็นอสมการสามเหลี่ยมจะอยู่ในลักษณะ p=q=2 เป็นความสัมพัมธ์จากการต่อเวคเตอร์เป็นรูปสามเหลี่ยมที่ n มิติ และสามารถใช้อสมการโคชี่ แก้การพิสูจน์ได้โดยง่าย








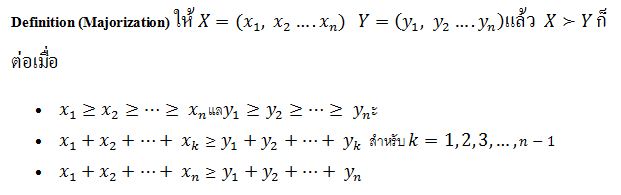
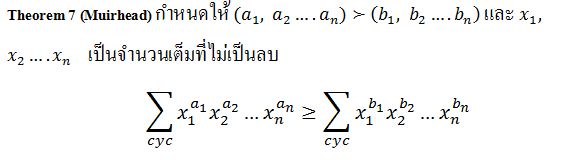









0 ความคิดเห็น:
แสดงความคิดเห็น